Deep Learning: Selected Ideas and Concepts

Thomas Keck (contact@tkeck.de)

Autonomous Driving


T. Pohlen, et. al. (12/2016)

Reinforcement Learning


N. Heess, et. al. (07/2017)

Speech Recognition & Speech Synthesis

Learn More

Reminder: Artificial Neural Networks

History

  • 1950-1970
    • Simple Perceptron without hidden layers
    • Assumed incapability to perform operations like exclusive-or (Minsky and Papert 1969)
    • Lack of computing power
  • 1980-2000
    • Invention of Backpropagation $\rightarrow$ Multi Layer Perceptrons
    • Assumed incapability to train many layers due to local minima in high-dimensions
    • Lack of computing power
    • Slowly superseded by methods like SVM and BDTs
  • 2000-2010
    • Dawn of Deep-Learning ($\approx 10$ layer networks)
    • Advances it algorithms (e.g. greedy layer-wise training, ReLU)
    • More statistics (big data)
    • Massive boost in computing power (due to GPUs)
    • Assumed that training even more layers is difficult due to vanishing gradient problem
  • 2010-2020
    • Deep-Learning (Representation Learning)
    • Batch Normalisation and architectures like ResNet allow for 1000 layer networks
    • Even more statistics (bigger data)
    • Massive boost in computing power (due to dedicated GPUs and TPUs)
    • Networks seem to be fundamentally flawed ($\rightarrow$ adversarials)

Deep Neural Networks
&
Vanishing Gradient Problem

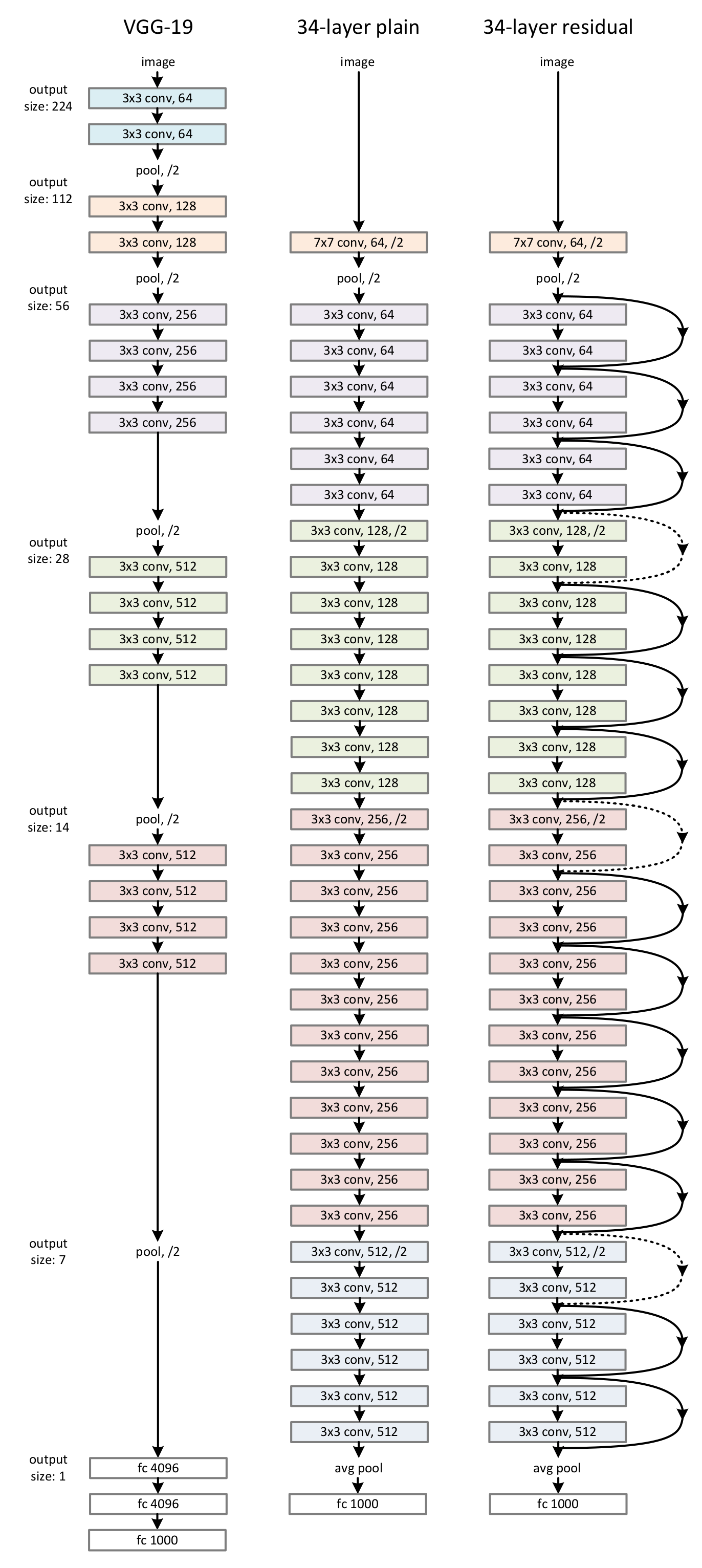
Example: ResNet

Techniques
  • ReLU Activation
  • He Initialisation
  • Batch Normalisation
  • Residual Network

34 layers (authors explored up to 1202 layers) used for image classification

Vanishing Gradient Problem

$$ y_{i+1} = \sigma \left(\sum^{N_i} w_i y_i \right) $$
Activation function is applied for each layer
$\rightarrow$ exploding or vanishing
activation
/
gradient

$$ y_n = \sigma \left( \dots \sigma \left( \dots \sigma\left( \sum^{N_0} w_0 x \right) \right) \right) $$
Training becomes unstable $\rightarrow$ very slow or no convergence

ReLU Activation Function

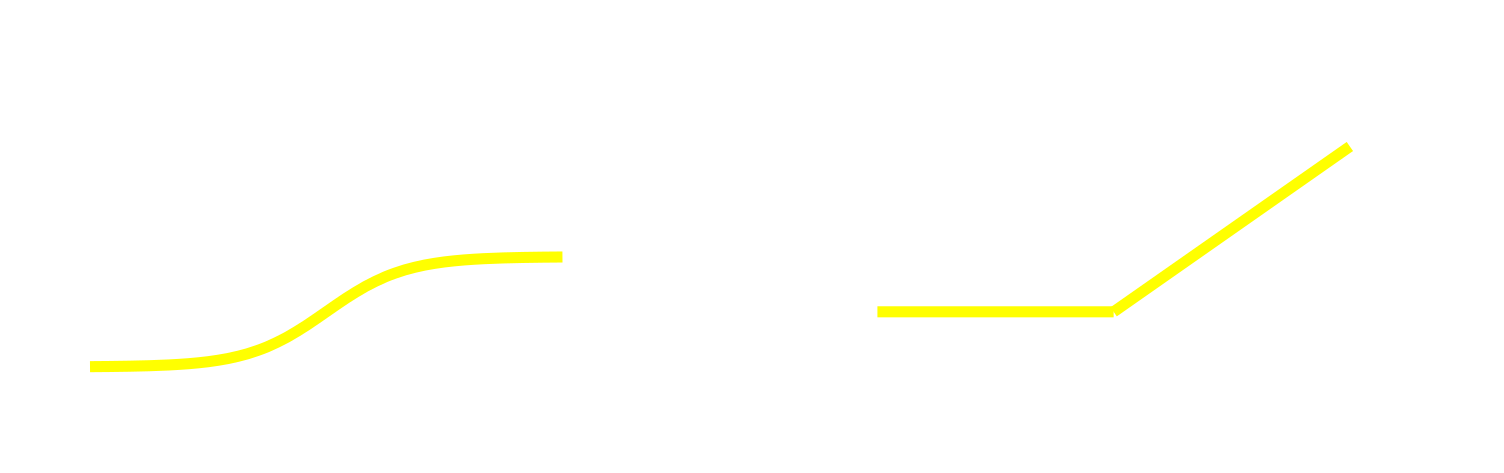
$$ \frac{\mathrm{d}}{\mathrm{d}x} \tanh = \frac{1}{\cosh^2} \le 1$$
Gradient vanishes in deep networks
$$ \frac{\mathrm{d}}{\mathrm{d}x} \max(0, x) = \left\lbrace \begin{array}{l} 1 \quad \textrm{for x } \gt 0 \\ 0 \quad \textrm{otherwise} \end{array} \right.$$
Gradient does neither vanish nor explode

He Initialization

$$ y_{i+1} = \max \left(0, \sum^{N_i} w_i y_i \right) $$
Weights can still lead to exploding or vanishing activations/gradients if
$$ \frac{1}{2} N_i \mathrm{Var}(w_i) \neq 1 $$
He Initialization (for ReLU)

$$ w_i \sim \mathcal{N}\left(0, \frac{2}{N_i} \right) $$ K. He, et. al. (02/2015)

Batch Normalisation

$$ y_{i+1} = \max \left(0, \sum^{N_i} w_i y_i \right) \quad \quad w_i \sim \mathcal{N}\left(0, \frac{2}{N_i} \right)$$
Weights are adjustable
$\rightarrow$ weights can still lead to exploding or vanishing activations/gradients
Batch Normalisation

$$ \hat{y_i} = \gamma \frac{y_i - \mathrm{E}(y_i)}{\sqrt{\mathrm{Var}(y_i)}} + \beta $$
  • Normalise inputs of activation function with respect to batch
  • Introduce learnable parameters to restore representation power
  • Regularizes the network (Dropout can be removed)

S. Ioffe, C. Szegedy (03/2015)

Residual Network

Idea: Split layer into
identity
and
residual

$ H(y_i) = $
$ F(y_i) $
$+$
$ y_i $

K. He, et. al. (12/2015)

Representation Learning

Why do we want to have a deep neural network?
  • distributed representations
    – the number of input regions which can be distinguished grows exponentially
  • depth
    – the ways to re-use learned features grow exponentially with the depth of the network
  • abstraction
    – the learned features in the deeper layers are increasingly invariant to most local changes of the input
  • disentangling factors of variation
    – the learned features represent independent properties of the input data

Convolutional Networks
&
Image Recognition




XKCD

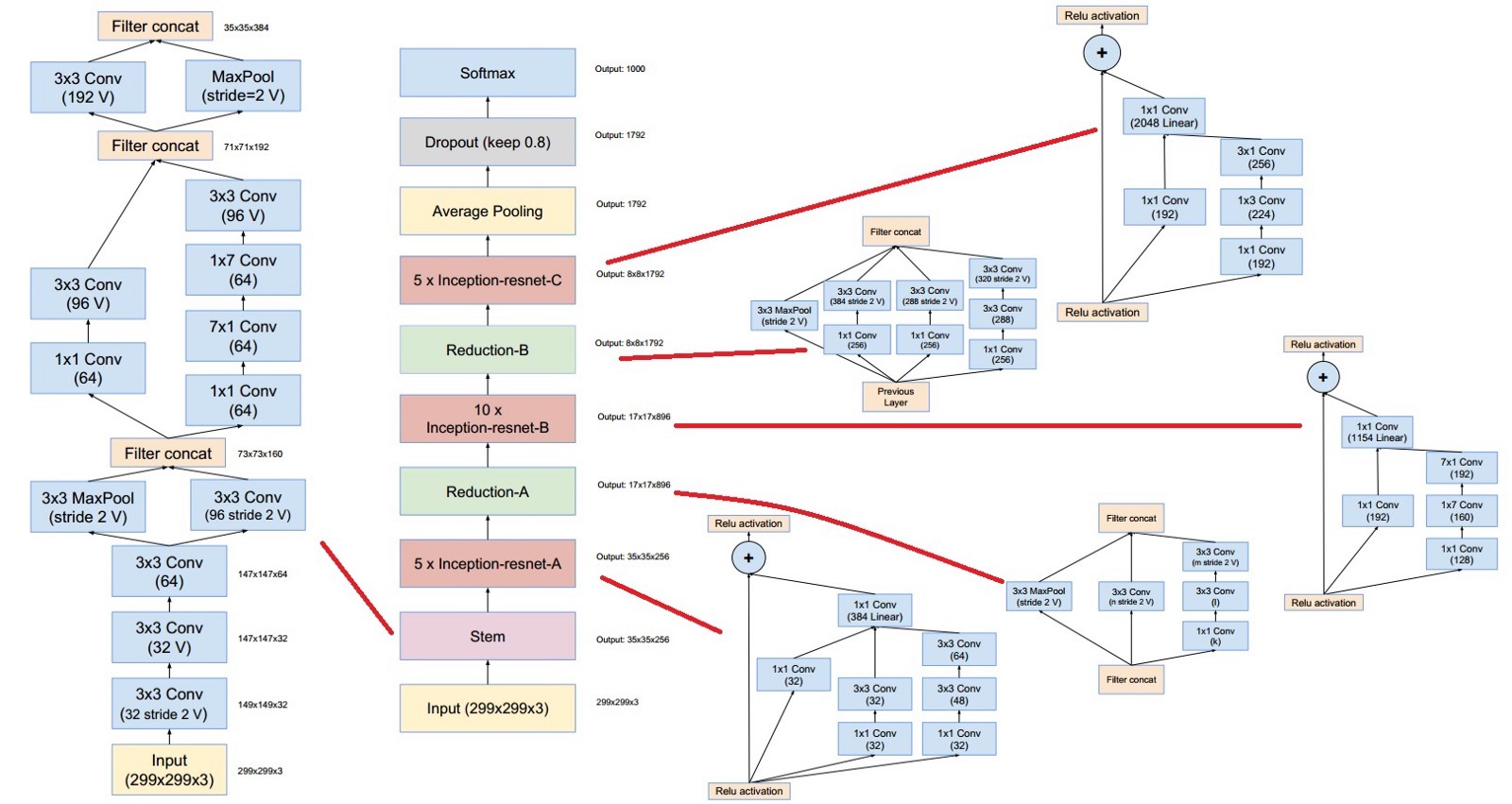
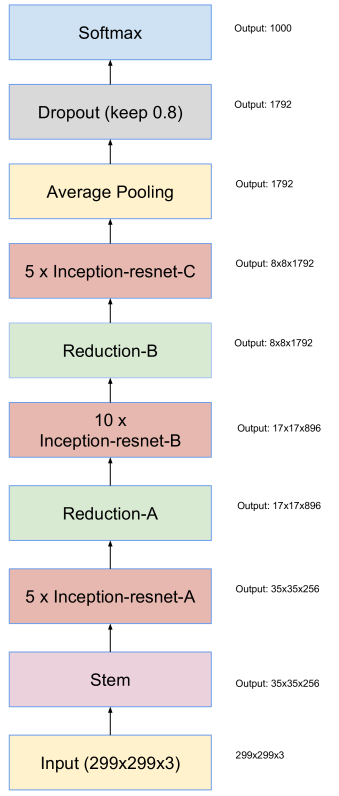
State of the Art: Inception-ResNet-V2


C. Szegedy, et. al. (08/2016)

Image Recognition

Multi-class classification task using softmax
$$ f(\vec{x}) = \underbrace{\frac{\exp \vec{l}}{\sum_{i=1}^{6} \exp l_i}}_{\mathrm{softmax}(l)} \quad \quad \textrm{where} \quad \vec{l} = \mathrm{NN}( \vec{x} )$$

Pixel Representation

Invariance under Transformations

Different strategies to build a classifier which is invariant under given transformations in the input space:

  • Extract hand-crafted features that are invariant
  • Use transformed copies during the training phase
  • Penalize change in the output under input transformation → Tangent propagation
  • Build invariance properties into structure of neural network →
    Convolution

Convolution

$M(x,y) = \sum_c \sum_{ij} $
$ K_c(i,j) $
$ P_c(x+i, y+j) $
Description
  • Learnable filters (e.g. edge detector) organized in feature maps
  • Each filter scans the image and detects a specific pattern
  • Convolution refers to the spatial dimensions
  • Input and outputs channels are still fully connected
Hyper-Parameters
  • depth – number of filters (also known as kernels)
  • size – dimension of the filter e.g. 3 × 3 or 3 × 3 × 4
  • stride – step size while sliding the filter through the input
  • padding – behavior of the convolution near the borders

Pooling

$M(x,y) = $
$ \max_{ij} $
$ P(x+i, y+j) $
Description
  • Takes inputs from small region in the feature maps
  • Reduces resolution and computation in following layers
  • Increases insensitivity against small shifts
Hyper-Parameters
  • depth – number of filters (also known as kernels)
  • size – dimension of the filter e.g. 2 × 2 or 2 × 2 × 4
  • stride – step size while sliding the filter through the input
  • padding – behavior of the pooling near the borders

Inception

Convoluted channels are still fully connected
  • For instance: Kernel size 3x3 with 100 input and 200 output channels
  • Many parameters (3x3x100x200)
  • High computational effort

$\rightarrow$ Most connections will be useless, can we do this in a sparse way?
Inception-v4 ResNet-v2 Module A
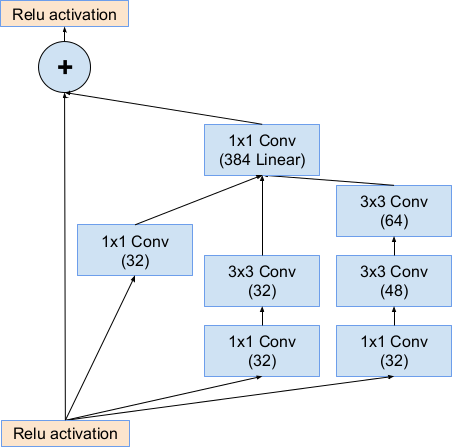
Inception
  • Use small kernels in parallel (3x3, 7x1, 1x7)
  • Bottleneck Architecture
    • Reduce number of channels before convolution (1x1 conv)
    • Restore number of channels after convolution (1x1 conv)

Global Average Pooling

Fully connected layers at the end are fully connected
  • For instance: 1792 Channels with a resolution of 8x8
  • Many parameters (8x8x1792)
  • High computational effort

$\rightarrow$ Most connections will be useless, can we do this in a sparse way?
Global Average Pooling
  • Position should be not important in the end
  • Take the average activation over the entire image
  • Reduces computation in following fully-connected layers

Regularization:
Dropout

Idea: Prevent overfitting by randomly dropping neurons during the training

Prevents co-adaption of neurons: G. E. Hinton, et. al. (06/2012)

Summary: Inception-ResNet-V2


C. Szegedy, et. al. (08/2016)

Recurrent Networks
&
Sequential Data Processing

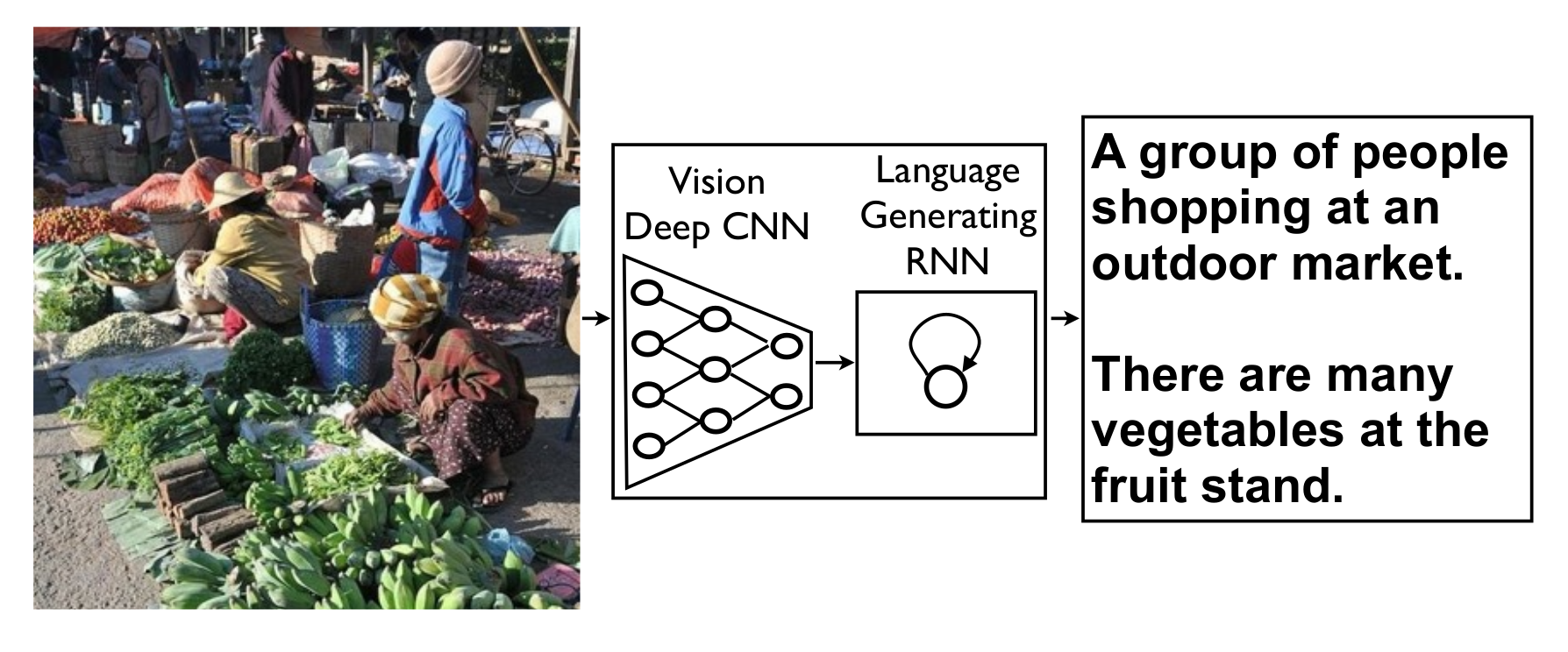
Example: Show and Tell


O. Vinyals et. al. (04/2015)

Recurrent Network

Recurrent Network

Recurrent networks contain loops;
last output of the neuron is used as additional input

Backpropagation Through Time


Wikipedia

Problem: Activation function will be applied iteratively ⇒ value (and gradient) vanishes or explodes

Solution: Long Short-Term Memory (LSTM) Cell


Wikipedia
Can remember a value for a long time period
  • Input gate decides when to update the stored value
  • Output gate decides when to output the stored value
  • Forget gate decides when to forget the stored value

One-hot Encoding

Howto turn text into numbers?
Categorial Mapping

$$ a \rightarrow 0 $$
$$ b \rightarrow 1 $$
$$ c \rightarrow 2 $$
$$ \dots $$
$$ z \rightarrow 25 $$
One-hot encoding

$ 0 \rightarrow $
$\left( \begin{array}{c} 1 \\ 0 \\ 0 \\ \dots \\ 0 \end{array} \right) $

$ 1 \rightarrow $
$\left( \begin{array}{c} 0 \\ 1 \\ 0 \\ \dots \\ 0 \end{array} \right) $

$ 2 \rightarrow $
$\left( \begin{array}{c} 0 \\ 0 \\ 1 \\ \dots \\ 0 \end{array} \right) $

$\dots$
$ 25 \rightarrow $
$\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \dots \\ 1 \end{array} \right) $

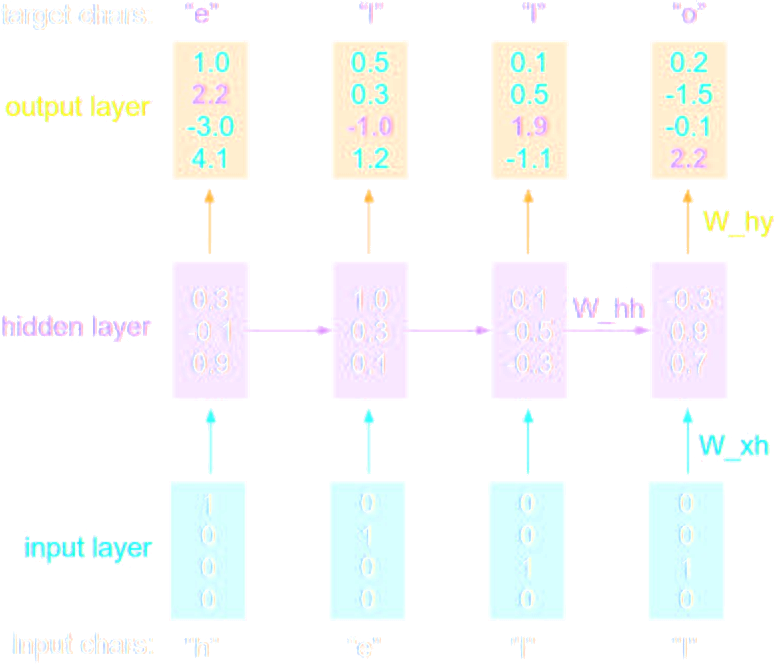
Example: Character-Level Language Model


A. Karpathy (05/2015)

Example: Character-Level Language Model


A. Karpathy (05/2015)

Example: Character-Level Language Model


A. Karpathy (05/2015)

Word Embedding

One-hot encoding works well for characters ($\sim 26$) but what about words ($\gt 300000$)?
$\rightarrow$
embed
high-dimensional
word
-space into low-dimensional space with neural network

Adversarials
&
???

Example: Adversarials in Image Segmentation


J. H. Metzen, et. al. (07/2017)
Adding
correlated noise
can change the output in an arbitrary way!!

Properties of Adversarials

  • Dense $\rightarrow$ easy to find
  • Artificial $\rightarrow$ do not appear naturally
  • Transferable $\rightarrow$ high probability to fool different networks
  • No effective defend-mechanism known

Goodfellow's Linearity Hypothesis

Neural Networks are too linear
I. J. Goodfellow, et. al. (03/2015)
Wiggle on one pixel of an image $\rightarrow$ taylor expansion of network:
$$ f(\vec{x} + \epsilon \vec{n}) \approx f(\vec{x}) + \epsilon \frac{\partial \mathcal{f}}{\partial \vec{n}}$$
Wiggle on $N$ pixels of an image in a correlated way $\rightarrow$ taylor expansion of network:
$$ f(\vec{x} + \sum_i \epsilon \vec{n}_i) \approx f(\vec{x}) + \epsilon \sum_i \frac{\partial \mathcal{f}}{\partial \vec{n}_i} \approx f(\vec{x}) + N\ \epsilon\ \bar{\partial f}$$
Even if $\epsilon$ is small e.g. 1px, we can change the outcome by $N \cdot \epsilon$ if we coordinate our wiggeling!

Off-Manifold Hypothesis

Adversarials are off-manifold.
T. Tanay, L. Griffin. (08/2016)
Number of artificial 800x600 images
: $N_A = 255^{800 \times 600}$
Number of natural 800x600 images
: $N_N \ll N_A$
Off-manifold one can easily cross a mis-aligned class-boundary

Example: Learning To Attack

Use neural network to generate adversarials!
  • Can be targeted to achieve desired mis-classification
  • Less salt and pepper noise
  • Interpretable changes to the image
  • Not transferable
S. Baluya, I. Fischer (03/2017)

Example: Adversarials for Humans and Computers

G. F. Elsayad, et. al. (02/2018)

Example: Adversarials in the physical world

A. Kurakin, et. al. (02/2017)

Solution: ???

Proposed solutions:
  • Augment training dataset with adversarials
  • Detect adversarials
  • Better regularisation
  • ...
Not completely understood and certainly not solved $\rightarrow$ very hot research topic!

Outlook
&
References

Outlook

There will be workshop on
Tensorflow
in the afternoon

References